A PhD's Apology

What follows is a slightly polished version of the opening statement for my PhD’s final defense, which took place on July 10th 2025. As mentioned That Day, this talk is dedicated to my favorite aunt, second mother and soul sister, Christina Papadopoulou, who passed away on December 29th 2024.

You can use this text to get to know me as well as idealloc, my most important professional achievement to date. If popularized treatments are not your thing, you may find a full technical report on idealloc here. Me myself am more interested in the philosophical stuff.

Prologue

I have been paying special attention to the games of Blackjack, Texas Hold ‘em poker and fellow gambling festivities that I indulge in with my childhood friends in the first hours of every New Year, gathered next to some fireplace in the village where I grew up. Whatever happens on the table that night seems to set the tone for the whole year to follow.

To give you an example, as 2024 was crying in its infancy, I ended up owning more poker chips than the total amount we had started the game with collectively. That mythical amount was agreed, according to our little loud economy, to be around 20 euros. I felt powerful for a while, until power turned into disgust. I caught myself being too excited about stripping whoever was next-in-line bare from their chips. Suddenly, I remembered that I had never wanted to spend that night competing against my friends; that I was decent enough to take all the wild fun I was having a little more seriously. I went all-in, and the only chip still with me when I got home was the one in my pocket.

My graduate studies that year followed this same course from hubris to humility. Scattered across diary entries, as well as in online discussions with colleagues, one can to this day find my old self announcing that 2024 was destined to grant me greatness. I would get published at ASPLOS, one of the premier conferences in my field, write the thesis, get the PhD. None of that happened. The only person from our house who graduated last year was my little sister. The only way I attended ASPLOS was by failing spectacularly at a co-located programming contest. 2024 taught me that neither was I the center of the world, nor did I want to be, or should be.

Before this year’s first dawn, however, the pattern shifted completely: again and again I played, again and again I lost. At the very last game I again nearly lost. When I was dealt with the winning card, my despair was so great that I didn’t even realize it! My friends had to step in and say “hey, Christos, you won”.

Thank you for honouring me with your presence here today. My name is Christos Lamprakos, and the research I shall present was done under the supervision of Prof. Dimitrios Soudris from NTUA, and Prof. Francky Catthoor from, back when I first met him, KU Leuven. I thank them from the depths of my heart for the trust they showed me and the wisdom they shared with me in the past six years. By the way, Francky, I wish to you a happy, active, unconventionally productive retirement, and hope for our paths to cross again, either thanks to your new role as Visiting Professor at NTUA or in whatever other context Lady Fortune deems appropriate. And to you, Prof. Soudris, I wish that the ecosystems you have built against all odds in your career, both professional and personal, keep thriving ever more over the years. My debt to you both cannot really be paid back.

The reason why I am talking as if this ceremony has already concluded in my favor is the joint co-operation agreement between NTUA and KUL, according to which the intermediate defense of my dissertation concerns the totality of my graduate work. Last May, in a sunny, suspiciously Greek version of Leuven, I did defend my thesis behind closed doors and in front of my appointed Examination Committee. After a long discussion, Prof. Hendrik van Brussel of KUL, acting as Chairman of the procedure, gave me permission to:

1. Proceed with today’s public defense.
2. Submit my dissertation’s text once and for all to KUL’s institutional repository, after acting upon the minor changes suggested by the Committee.

These facts of course do not give me rights to use the “Dr.” prefix in everyday life just yet. There is a formal, strict procedure to be followed here too, only at the end of which can a final, official decision be made. Nevertheless, it is these same facts that give me enough courage to take an unorthodox course of action for my opening statement.

I will not try and fit six years of research in 35 minutes in a way that can satisfy a general audience; an audience joined even by my dear Mom, who is already confused enough thanks to the language I must speak. I will focus instead on the most mature, and thus most useful part of my research, described in the fourth chapter of my dissertation.

That chapter is the reason why I do not feel ashamed to be standing in front of you today. It goes without saying that I am ready to defend any other part of my thesis the Committee deems necessary to discuss. For now, however, I kindly ask you to bear with me.

Introduction

Let us start by introducing our topic.

We shall concern ourselves with static memory planning. Static memory planning is a refined version of the Tetris videogame. Tetris presents players with a sequence of bricks of various shapes and sizes. The bricks appear at the top of the screen and slide downward, until they either bump on some previously placed brick or reach the ground. At that point the brick is considered placed and cannot be moved any more. Then the next brick appears at the skyline, and so on. While bricks are still falling, the player can move them left and right. The goal is to place as many bricks as possible without ever touching the skyline. At all times, the player gets a sneak peek of the next brick scheduled to appear after the current one.

As everyone who has needed to pack their suitcase for a trip knows, the main enemy of all packing is unused space between items. At the scale of a weekend escape, the price of that unused space is being unable to bring an extra sweater along with you. At the scale of an international giant whose business to a great extent relies on packing as many boxes per truck as possible, wasting space is simply unacceptable. The technical term for wasted space is fragmentation. Static memory planning is a refined version of Tetris; both tasks are packing operations; the Holy Grail of packing operations is to eliminate fragmentation; fragmentation is a fancy name for wasted space; space is considered wasted when it exists but is not utilized.

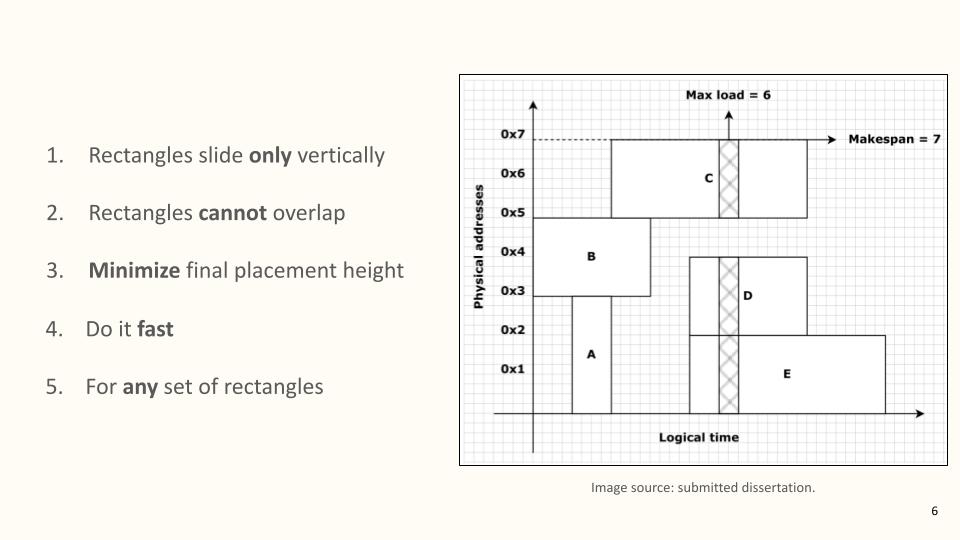
Let’s be specific about all this. An instance of static memory planning comprises a set of rectangles on the two-dimensional plane. The vertical axis is interpreted as memory, that is, a contiguous range of space. Rectangles can slide up and down the memory axis while searching for an optimal placement. The horizontal axis stands for time: rectangles cannot slide across that axis. The coordinates of the left and right endpoints of each rectangle form part of its identity. They cannot be changed, in the same unfortunate sense that we cannot change our birthday, our height, or the time that the sun will set this afternoon. A solution to an instance of static memory planning is an arrangement of the input rectangles across the vertical axis so that:

1. No two rectangles overlap.
2. If we drew a rectangle around the whole arrangement, the height of that rectangle would be the smallest possible.

I remember myself three years ago during one of our weekly updates with Francky, claiming I had learned and done all there is to learn and do around static memory planning. That I would soon proceed to cooler stuff. It is fair to call that past self naive and arrogant, sure, but don’t you agree that this figure looks too simple? I swear to you, I haven’t hidden any of the absolutely necessary information one must have on static memory planning. Slide rectangles vertically to pack them as tightly as possible while avoiding overlaps. That’s all.

However, necessary things are rarely enough in a competition. A definition of a PhD that has stuck with me ever since I read it is “become the best in the world in a narrow area of specialization”, which is another way of saying “compete against anyone who has tackled the same problem before you”. Under such high stakes, focusing on the first three rules is like coaching a hundred-meter sprinter for the Olympics and insisting that all they have to do is follow a hundred meter straight line to its end. The real challenge in static memory planning is to do the job fast, and do it for any possible set of rectangles. We know for a fact that adding these last two points in the mix makes static memory planning one of the hardest problems in computer science. There is no optimal algorithm for packing all possible sets of rectangles wasting minimum space in minimum time. Formally, static memory planning is NP-complete.

What computer scientists do with NP-complete problems is, they devise “good enough” algorithms instead of optimal. We call these approximate algorithms. The best known approximate algorithm for static memory planning appeared two decades ago. Now these guys were mathematicians, while I was… nobody, really, but a nobody who liked programming and, above all else, a nobody who must graduate. Anyway, I contacted them and asked if anyone had ever bothered to turn their mathematics into a real computer program. They answered that no, nobody had, and wished me good luck. Thus my plan became just that: implement a static memory planning agent in code, publish it, get the PhD. Use the Rust programming language for the task. I laid that plan halfway through my studies, three years ago. I thought I would soon be done with it.

What happened instead was, reality chose to strike all of the arrogance and naive thinking out of my soul through a series of failures, false wins, and of course rejections from ASPLOS. I had to write my program from scratch three times before making it work good and fast for any input. All of my prior assumptions about computers, mathematics, research, myself, other people, life and destiny were crushed in the process.

This process produced several artifacts. I created idealloc, the only static memory planning implementation out there that can handle any input set of rectangles fast with minimal fragmentation. I also verified the correctness of idealloc’s base algorithm by hand, and made crucial extensions to it. I gathered a variety of insights on the design and implementation of static memory planning programs, on which future researchers can support their own work. I conducted the first rigorous and comprehensive evaluation of existing solutions, and last but not least, I created the first truly challenging benchmark suite for the task.

But why should you care about all this? Apart from Christos getting his PhD, is there any serious motivation behind this static memory planning business? To be honest, I disagree with this line of thinking. In my view I have already laid out enough motivation: a large body of theoretical work on an NP-complete problem, little to no real-world implementations, let’s build one and see what happens. Anyway…

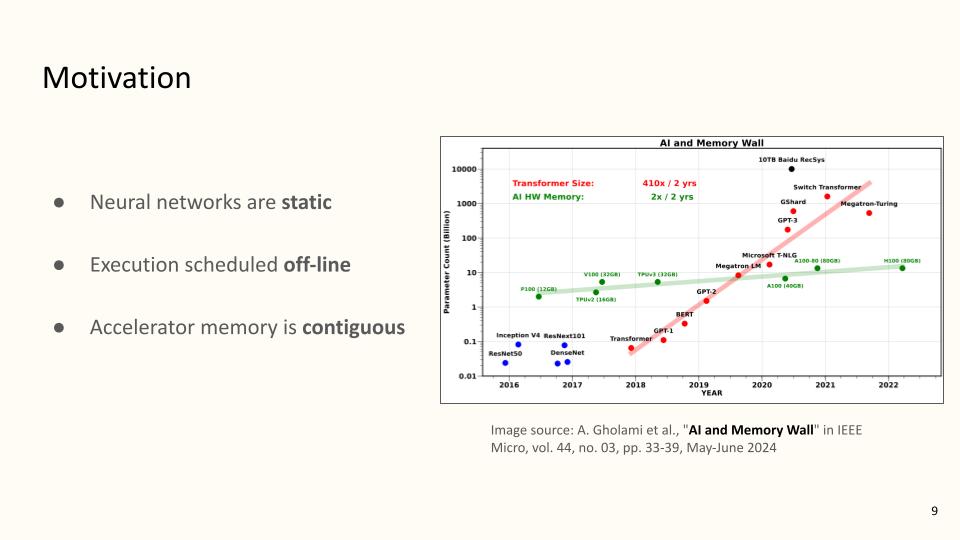
In a coincidence good enough to qualify as a work of Divine Providence, there is some “concrete” motivation for static memory planning indeed. It turns out that nowadays neural networks, that is, the basic components of popular tools like ChatGPT, make a lot of money. Deploying neural networks efficiently is a major concern for whoever gets that money. Tons of research has been devoted to this task, and people have come to agree that traditional general-purpose hardware like the computer I’m using right now for example, is not the way to go. Instead, we use devices called accelerators, specially designed to align with the architectural characteristics of neural networks. One such device is the GPU, and to get a grasp of how much money is involved in this game, you can do a google search for NVIDIA’s market cap (or, rather ironically, you could ask ChatGPT). What you need to remember is, running neural networks on accelerators entails a series of memory operations, and these memory operations can be expressed as instances of static memory planning. The size of neural networks, and consequently the memory they require, grows many times faster than the memory capacity of the hardware used to run them. Sooner or later, the people with the money will notice.

For now, however, they haven’t really. There are a couple of explanations. First, the bottleneck that models like ChatGPT are facing for now concerns dynamically managed memory, which is the formal way of saying that one does not know the future. The term “static” in static memory planning is the opposite of “dynamic”, and thus means that we do know the future, in the form of co-ordinates on the horizontal time axis shown earlier. Another reason is that, again for now, real-world instances of our problem contain thousands of rectangles at most, and there the state of the art behaves decently. The word “Futureproof” in the title of this talk on the other hand, anticipates millions of rectangles–and beyond.

Let us now turn to what our competition does. A most striking observation I made early on was that approximate algorithms such as the one I used for idealloc’s foundation are ignored completely. Instead, practitioners go for either fast and scalable heuristics, or low-fragmentation but risky isomorphisms. Let’s say a few words on each of these two terms. In general, heuristics are simple rules without strict mathematical underpinnings believed to work “well-enough” most of the time. In our context, I define a heuristic as a two-step operation comprising (i) a sorting step and (ii) a placement step. The first step is self-explanatory: rectangles are put in sequence according to some criterion, for example decreasing height. During the second step, the sorted rectangles are traversed in order and placed in a best- or first-fit fashion.

This is the pseudocode for first-fit placement: its main idea is “scan the address space bottom up and put the next rectangle in the first big enough gap that you find”. Without being able to prove it, I think people use heuristics when they are not willing to invest significant effort on more complex and risky approaches. Isomorphisms, on the other hand, is a deliberately generic term on my part. In mathematics, an isomorphism is the translation of a problem into another problem. A popular isomorphism for static memory planning in the special case that all rectangles have the same vertical height is interval graph coloring, which by the way can be solved optimally. So why do people choose to formulate static memory planning as other problems? My explanation is similar to the one I gave for heuristics: some isomorphisms employ well-established methods and tools that allow a black-box treatment of the problem, in turn minimizing the required engineering effort, and also giving the opportunity to exploit existing domain knowledge. Both approaches benefit from the small scale of present instances. As my results show, however, both approaches collapse when this scale becomes large. Instead of futureproof, they are secretly fragile.

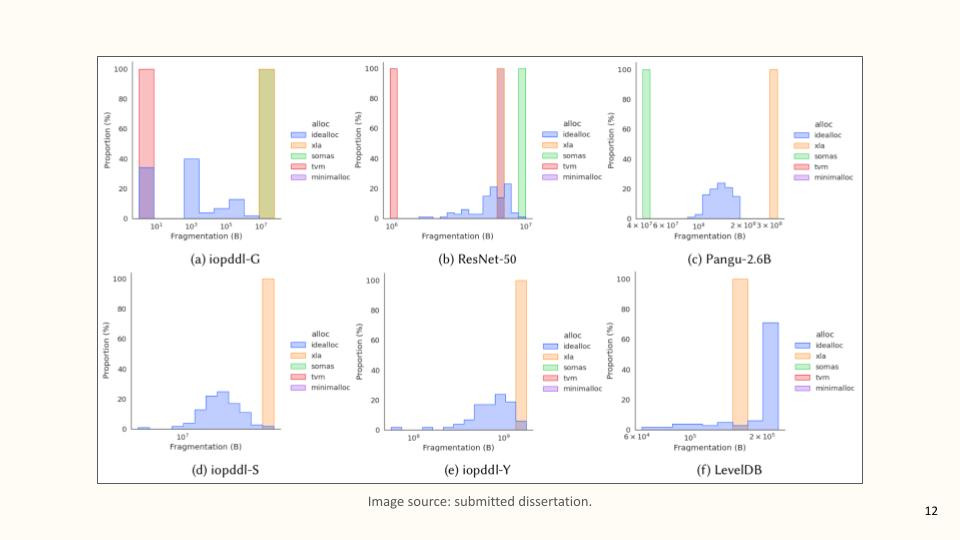
And since we’re talking about results, let’s use some evidence to back my claims. What we have here is six histograms. A histogram visualizes the distribution of data. In our case, that data is fragmentation (recall that this means wasted memory). Each colored bar in the histogram represents a different static memory planning implementation. The blue one is idealloc, my solution. The orange one comes from XLA, an open-source project backed by Google. XLA uses a heuristic. The green one, SOMAS, was published by researchers from Huawei. SOMAS executes multiple heuristics and picks the one yielding the lowest fragmentation. In red we have an isomorphism-based solution from TVM, a deep learning compiler from the Apache Foundation. And finally in purple, we have minimalloc, another Google project which is already deployed in the company’s Pixel devices. minimalloc also uses an isomorphism. Each histogram corresponds to a different benchmark, a different input set of rectangles. The more to the left a bar ends up along the histogram’s horizontal axis, the better it performed in terms of fragmentation. We see for instance that the solution by TVM delivered zero fragmentation in the top left benchmark. XLA wasted gigabytes of memory at the bottom center benchmark, and so on. The following points can be made here:

1. Some implementations are missing from some benchmarks. They are missing because they either crashed or timed out. Only idealloc and XLA participate everywhere.
2. No solution is best in every benchmark. XLA and SOMAS, which are heuristics-based, waste the most memory most of the time.
3. Only idealloc has consistently the lowest, or second-lowest, fragmentation.

Another observation is that idealloc’s fragmentation is spread along the horizontal axis instead of accumulating into a single bar. In other words, idealloc’s behavior is non-deterministic (but not random). We can return to this point later. For now, I hope to have convinced you that, if nothing else, my work at least stands firm against its peers.

Boxing

But how does it do it, really? Beyond any doubt, idealloc’s greatest intellectual debt is owed to the algorithm which forms its beating heart. Let’s take a look.

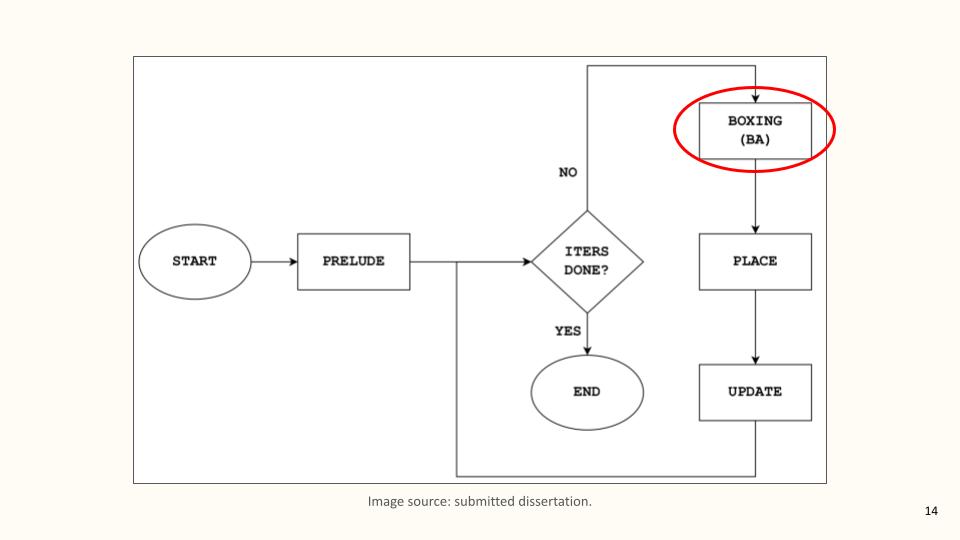
In fact, let’s first get an idea of the entire body before focusing on its heart. As you can see, from a high level idealloc is not that complicated. There’s a pre-processing step for safety checks and expensive data pre-computation, and then we go into a loop controlled by a user-provided total number of iterations. Each iteration comprises three steps: (i) boxing, (ii) placement, and (iii) potential update of the solution if a better result is found. I can later guide you through all of that, but my priority for now is the boxing algorithm. I shall be referring to this algorithm as BA, which stands for “the boxing algorithm by Buchsbaum and his colleagues”.

As mentioned earlier, the NP-completeness of static memory planning has led researchers toward approximation algorithms. The quality of each algorithm is expressed as upper bounds for fragmentation. For instance, a 6-approximation algorithm guarantees that it will never waste more than six times the memory that is absolutely necessary. The best known algorithm for static memory planning is BA: a (2+ε)-approximation technique published in this paper called “OPT versus LOAD in dynamic storage allocation”. By the way, dynamic storage allocation is, in this context, synonymous with static memory planning. Do you see the contradiction between using the term “dynamic” for a static problem? Considerable confusion, and, in my view, real damage to research is owed to this naming decision. Most computer scientists out there interpret “dynamic storage allocation” as a relevant but different problem, which is the real-time management of memory in operating systems like Windows and Linux. These same people have never heard of static memory planning–and yet, a key insight of my PhD is that static memory planning can help us study and improve real-time memory management. As most things in computer science, this is not a new idea. The sages who coined the term in the sixties did so precisely because studying on-line memory management in an off-line substrate, where by definition the future is known, can be expressed as static memory planning. You can read the whole story in Chapter 3 of my dissertation. For now let us return to BA.

The most important thing to understand about BA is that it is incomplete. In the two-step heuristics terminology introduced earlier, BA is a partial sorting step. It accepts a set of rectangles as input, and yields a new set of rectangles as output. A more convenient name for the output rectangles is “boxes”, since the main idea of BA is to group rectangles together into new, enclosing rectangles. This by the way happens recursively. Boxes contain other boxes, and so on until some level of depth where subsets of the original rectangles reside. The authors of BA build their whole paper on this boxing operation, since it allows them to draw upper bounds for fragmentation. Given the fact that they are mathematicians and not programmers, this is enough for their needs.

But a poor programmer like myself was surprised to find that, instead of a full solution to static memory planning, what one gets by implementing BA is not far from this cute set of Russian Matryoshka dolls. Still, a nice implication is that boxing protects us from what we call a combinatorial explosion, that is, programs that crash out of memory or take forever to terminate because there are just too many possible scenarios to evaluate. The four rectangles on the left of this figure can be ordered in 24 different ways. By boxing them into the two red rectangles on the right, we reduce possible orderings by a factor of 3. We have, as we say, pruned the search space of the problem.

Now let me be more specific about what I mean when I say that I have implemented BA. Like any work of mathematics, BA is full of lemmas, theorems and corollaries. I will be referring to these constructs collectively as functional units. Each functional unit starts with a statement, and then presents a proof testifying to the correctness of the statement. Lucky me, every proof in BA is given by construction: each step either calculates something, like for example, “compute the ratio of maximum to minimum rectangle height”, or invokes some other functional unit. Of course, there are additional mathematical arguments in between which cannot be turned to computational logic. These can be omitted as long as one knows what they are doing. To give you a concrete example, here’s Corollary 17 from the original paper, which I initially mistook for BA’s entry point.

From a programmer’s perspective, the interesting pieces are what I’ve marked in red. Corollary 17 can be seen as a function which expects a set of rectangles as input. Note that BA refers to both original rectangles and boxes as “jobs”. The body of the function for Corollary 17 is a mere invocation of another function, named Theorem 16, using a specific value as argument to a parameter named epsilon. A large part of my work, then, was to read each functional unit, understand it, isolate all steps in it that can be converted to code, write the code, and test the code. One of the comments I received from the Examination Committee in May was that I do not simplify this process enough for the Reader. I wish I could make it simpler, but I cannot. If you are lucky, you can avoid the pains that come with cooking your favorite meal–but in the end you will have to invest the effort required to eat it.

What I can do is assure you that my work is not a mere implementation of some existing algorithm. First of all, the functional units of BA as a whole do not even qualify to be called an algorithm. Algorithms must be simple and correct; BA is a complex system of operations, partly recursive, partly parallel, partly stochastic, and most importantly, partly wrong.

As this Table shows, I intervened in several parts of BA to make it functional. I verified it formally by hand, only to discover that additional conditions must hold for the process to converge. I introduced novel algorithms for unboxing the Matryoshkas that BA yields and delivering a real solution to any instance.

Several other interventions were needed, both on the high level of algorithms and control flow (I have listed some examples on the left column), and the low level of mechanisms and data structures (respectively on the right). It was only after I combined all of these, at the third iteration of building idealloc from scratch, that I beat the state of the art.

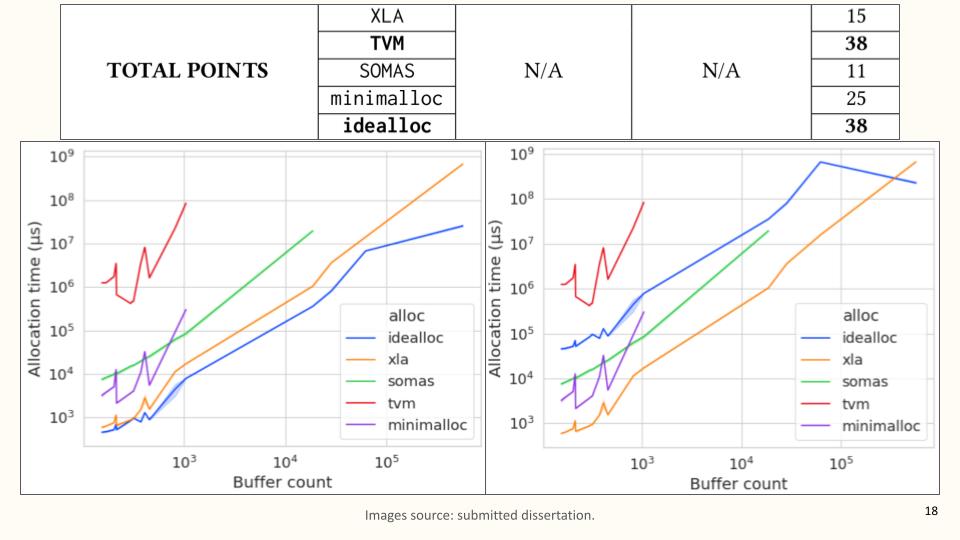
I have repeatedly made this heavy claim of beating the state of the art. I’ve shown a couple of histograms, but so what? People in our field love numbers, so let’s look at some numbers. Imagine that each benchmark of my experiments, each set of rectangles, is a race. Many races together form a tournament. Imagine that each of these five static memory planning implementations is a contestant in this tournament. Contestants gather points after each race, according to their finishing position. The table in this slide shows the total points each contestant got after seventeen races of varying difficulty. idealloc achieves top score. In fact, TVM achieves top score too; recall that it implements an interesting hill-climb optimization isomorphism. But as I said earlier, isomorphisms are not scalable.

To get a clear impression of this point, let’s look at how much time each contestant needed to produce a solution as the number of rectangles per benchmark increased. TVM and minimalloc, the two approaches using isomorphisms, cannot handle more than a thousand rectangles at a time. XLA in contrast, using one single heuristic, is the fastest, and keeps a steady behavior up to half a million rectangles. What about idealloc? You may recall that idealloc operates in a best-effort fashion: it executes the boxing-unboxing-placement cycle many times, and keeps the result with the lowest fragmentation. Two questions must be made here: how fast is each single iteration, and how fast does the whole thing behave. On the left we see that each idealloc iteration is the cheapest in terms of time needed, regardless of the number of rectangles. On the right we see its total time per benchmark. All of the following points are fair:

1. idealloc’s users can rest assured that they pay the minimum amount of time per iteration.
2. Faster heuristics exist, but they suffer from high fragmentation.
3. More memory-efficient isomorphisms exist, but they suffer from lack of scalability and high latency.

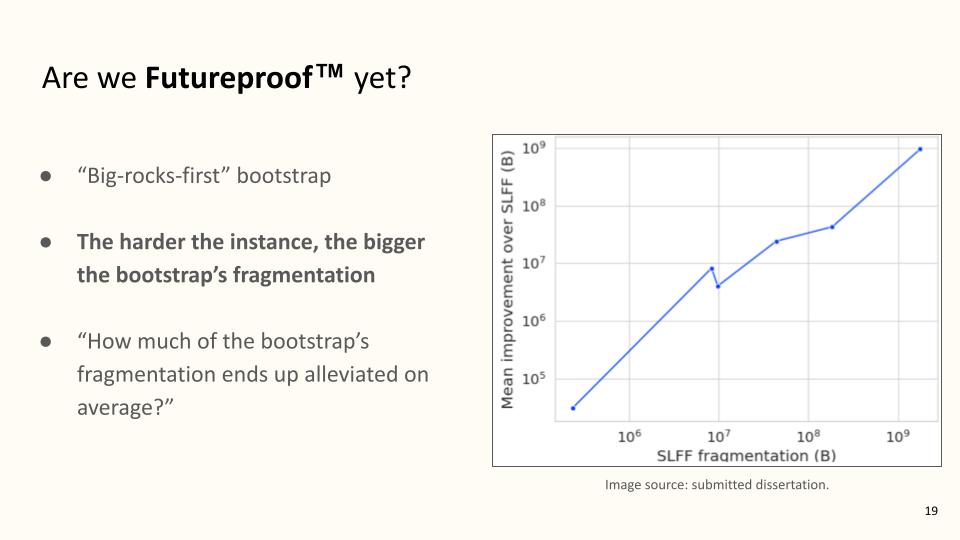
There’s one last point to make. The title of my talk starts with the word “Futureproof”. What does this word mean? Because if I’m right, very hard static memory planning instances are on the way. A futureproof solution must deal with arbitrarily hard instances well. But what makes an instance hard? It cannot be simply the total number of rectangles, since it is easy to imagine millions of rectangles with trivial-to-handle lifetimes. My proposal is simple: an instance is hard to the degree that a heuristic-based solution is fragmented. To understand my point, imagine this: a simple heuristic for packing your suitcase is to start with the biggest items. If you manage to put everything inside, your stuff wasn’t hard to pack. Else your stuff was as hard to pack as the volume of stuff you were forced to leave outside. I have applied this concept to idealloc. A central pre-processing step is to run a “big-rocks-first” heuristic on the input, where I sort by size, break ties by lifetime, and do first fit. Each next iteration of idealloc must outperform this bootstrap, else it breaks the loop early and tries again. So two solutions of interest are produced every time we run idealloc: the “big-rocks-first” one, and the best one, that is, the one finally returned to the user. In my view, idealloc is futureproof to the degree that its best solution eliminates the fragmentation introduced by its bootstrap heuristic. So how does it fare?

According to this figure, my favorite figure from the whole text, idealloc fares well enough. The optimal behavior would be the identity line, but, firstly, that would make idealloc perfect–and perfect things do not exist in the material world–and secondly, this line and the identity line are not very far apart. This result concludes my technical exposition on Futureproof Static Memory Planning. idealloc’s source code, benchmarks, and the technical report on which this talk is based, have already been made public.

Epilogue

I, however, am not done. The very naming of the title I have been striving toward exerts on me an irresistible force. You see I pride myself in taking words seriously, and have many times paid the price for my pride. But what God made crooked, no one on this Earth can make straight.

I thus ask you to indulge me a couple minutes more, so that we may all contemplate this funny little phrase, “doctor of philosophy”.

The first thing that people obsessed with words do is look them up in the dictionary. Let’s do that for our case. “Doctor of philosophy: the highest degree awarded in many academic disciplines”. Well this is rather obvious. Second meaning: “a person who has earned the academic degree of doctor of philosophy”. So a PhD is both the title and the person holding the title. Does that satisfy you? If you’re me, it doesn’t. It’s too self-referential. Wikipedia says that the first PhD ever was awarded in 12th-century Paris. Why did those people, almost a thousand years ago, choose these specific words for this specific title? There must have been a reason, don’t you think?

Let’s take each word separately. Wikipedia again: an academic title that originates from the Latin word of the same spelling and meaning. The word is originally an agentive noun of the Latin verb docēre–“to teach”. Well that’s something.

Let’s cross-check with Merriam-Webster: indeed, the dictionary accepts this meaning. A doctor is then, in the academic context, a teacher. A couple more interpretations are also interesting: a person skilled or specializing in healing arts. A person who restores, or fine-tunes things. If I had a gun to my head I’d swear I see a pattern here. A common divisor.

Teaching, healing, fixing, tuning. Can you see it? It’s alright if you don’t, because I may as well be wrong. But until I’m proven wrong, the pattern I see is that of Order. Order as in the opposite of Chaos. A teacher puts order in their student’s knowledge. A healer brings an organism back from some disintegrating sickness. A fixer restores a mechanism’s principle of function. A tuner helps one focus in one specific area out of many. Each image is a distinct reflection of the same face. Doctors fight for Order, not in the sense that a policeman does, but rather like someone on duty against entropy, against Chaos and the Great Death of the Universe.

At the end of the day, like the great British show asserts, a Doctor is a force for Good. Now I am not foolish enough to ascribe such high qualities to myself, though I do indeed try to be good. No, there has to be something else–and I think there is. Remember the first dictionary definition for a PhD? The one I dismissed as too self-referential? It said that a doctor of philosophy is at the same time the holder of the thing, and the thing itself. So this idea about re-establishing Order, about being a force for Good… I find it more fitting and more useful to ascribe these features to the process instead of the product. I can assure you that in my case, my graduate studies have indeed put my life in such a blissful, incomprehensible Order as none that I could ever imagine. The man speaking to you today is not the same person as the one who knocked on Prof. Soudris’ door so long ago, and if I do not credit this transformation to the PhD, the thing that became the very fabric of my life, I do not know where else to look. In case you were wondering, now I’m satisfied. With the first half of the title, that is. But as you may have guessed already, the first half is not what I’m really into.

Lady Philosophy, then. A PhD makes one a Doctor of Philosophy. The Wikipedia entry says that again, in an academic context, “philosophy” is meant as the love of wisdom. Take it all together and we have a Doctor of Philosophy as a teacher of the love of wisdom. What is love though? What is wisdom? We will never find the time to unpack these two. We need something better, something more compressed. Luckily, I have been curious about this question for a long time before starting to write this talk. Moreover, this is the place I wanted to reach ever since I started writing this talk. The biggest research question of all. What is philosophy? Here is my answer:

1. Philosophy is the art and discipline of living well.
2. To have lived well is to look back, right before the end of your life, and find in what you see the courage to face death. A life well lived is a life left behind peacefully.

I don’t know where I stand with respect to this definition. It is impossible to know. But as far as my student self is concerned, that once young, romantic soul who thought he could thrive in this world just by reading books one after the other, that little man has now reached the end of his life. So allow me to ask him for you: have you lived well?

Yes I have. Thank you for your attention.